Last year I set three goals for myself to work on over the course of 2019:
- Stream on Twitch during the week
- Write one blog post a week
- Finish reading Deep Learning by Ian Goodfellow
Goal 1: Stream on Twitch on weekdays
Result:
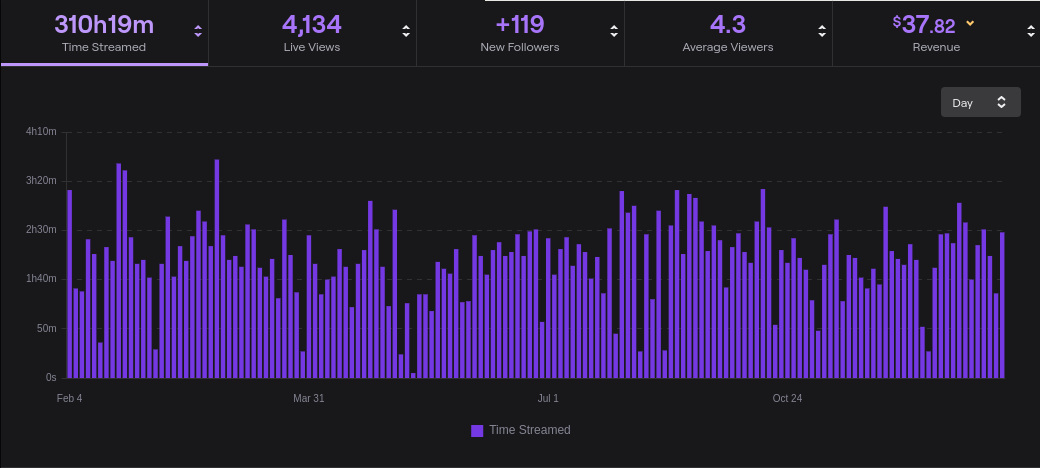
I can’t figure out how to get a “days streamed” metric out of Twitch, but the above suggests I did alright. There were a few periods in June and August where I took breaks from streaming but I’m pretty happy with my overall consistency.
I made a grand total of $37.82 over the year which works out to about 12 cents an hour!
In 2020 I’d like to continue streaming and will stick to the same schedule.
Goal 2: Write one blog post a week
Result: 12 posts / 52 weeks
So this is the second year I’ve hit about one blog post a month and been completely unable to maintain a pace of one post per week. There’s probably a few reasons for this but in general I haven’t come up with a good “series” of blog posts that I can consistently churn out.
For this reason I’m not going to renew this as a goal for 2020.
Goal 3: Read Deep Learning by Ian Goodfellow
Result: 700 pages / 700 pages
So this was pretty much a complete success. As I mentioned in last year’s retrospective the initial two chapters were intimidating but the rest of the book was not nearly as hard to get through. I wrapped this one up fairly early in the year and while I didn’t read any other books, I’ve started to become confident at reading papers themselves.
Overall I’m not sure if I’d recommend this book to a new learner in 2020. Lots has changed in the years since it was written and some of the off-hand recommendations in makes actually turned out to be incorrect. That said, if an updated version is ever released, I will definitely read it.
Other stuff I did in 2019
There were a lot of non-goal tasks that I worked on throughout the year:
fastai – I worked through the first course during January and was invited to participate in the second course in April. I wish I’d found this course earlier since it really got me started on tackling both deep learning papers and real world projects.
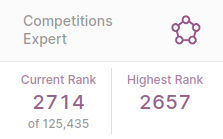
Kaggle Competitions – After completing fastai’s courses, I worked on my first four Kaggle competitions and got progressively better placements on each. In total I received two bronze medals which moved me up to the rank of Kaggle Competition Expert.
Paper Reading – In general I became much more comfortable reading papers. My favorites were Mixup: Beyond Empirical Risk Minimization and Bag of Tricks for Image Classification and Convolutional Neural Networks.
Visualizing RNNs – I worked on a cool little tutorial that visualizes each step of an RNN. The post is available here.
Goals for 2020
Overall I’m very happy with how 2019 went. While there was room for improvement it felt like things having been moving in the right direction. With that in mind I’d like to set a few goals to keep me moving in that direction:
- Stream on Twitch every weekday
- Get one gold medal on Kaggle
- Create one deep learning video each month
- Either get a job in deep learning or start a company around it